EMC関連のセミナーを聴講させて頂くと、よく講師の方が下図のようなマイクロストリップ線路のモデルを示して、電源ラインや信号ラインの形態で活線に対向するGND電極パターンで活線(ライン)方向に対する幅方向の長さ(幅)は広い程よい、という説明をよくされます。
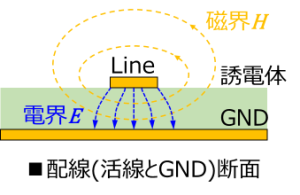
理由として、
①GND電極パターンにより生じるインダクタンス成分を逓減できることにより、
②GND電極パターン全体の電位を0Vに近づけることができ、
③GND電極パターンにより生じる不要輻射(EMI)を低減できるから、
等と解釈しているようです。
一般的なEMCを担当されている方々は、素直に納得してしまうかもしれません。でも、これって本当なのか、と疑ってみるのも自身のスキルを高めるために必要かもしれません。
そこで電磁界Simを使って伝送路に於ける電流・電圧分布の状況を可視化してみました。伝送路のモデルとして屈曲部を持つ長さ300mmのマイクロストリップライン(伝送路)を活線側の幅を0.2mm、GND側を(1) 幅200mmのベタパターンと、(2)幅100mmで活線側に合わせて切り欠きのあるパターンとして、それぞれのモデルの誘電体厚みを0.1mm(4層基板の表面層を想定、下図参照。)としてSim計算してみました。
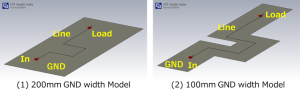
下図は100MHzでの(1),(2)モデルのGND電極に於ける電流分布を示しています。(1),(2)モデル共にGND電極上で活線と垂直に対向した領域に電流が分布した状態となっており、(1),(2)モデル共GND電極の幅方向の端部の電流分布は殆ど0に近い状態となっています。
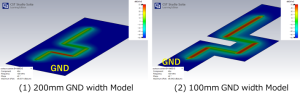
ここで先ず、確認しておきたいことは電流分布があるということは電位(電圧)があるということであり、電流分布が無いということは電位が0Vということになります。即ち、電流は電荷の移動であり、電荷があるということは電圧を持つことを意味するからです。従いまして、AC(高周波)であれDC(ACの周波数を0に近づけていってもその途中に特異な特性上の変化点は無い)であれ、活線と対向するGND電極の領域には電圧(活線に対して反対極性)が生じ、その他の領域で電位は0Vに近づきます。
ということで、上記②で述べたGND電極パターン全体を0Vに近づける、というのは現実とは異なる考え方なのです。そもそも活線側に信号(高周波)や電源の電圧がかかっているのにその対向側が常に0Vという考え方は電気回路学のような伝送路の長さ・形状を考慮しない回路モデルの考え方であって、その考え方をそのまま現実の回路に当てはめるのは適切ではないのです。
また、前述の①に述べたGND電極のインダクタンス成分に関しては、(1)、(2)のシミュレーション結果から(2)の伝送路の伝送路インピーダンスが大きくなる傾向になっており、GND電極の形状による伝送路インピーダンスへの影響はあると考えられます。しかし重要なことは活線とGND電極が常に対向した形態で伝送路において連続し且つ維持された状態となっていることで、(1)、(2)のシミュレーションでの伝送路における各周波数での損失は下図に示すように略同等となっています。
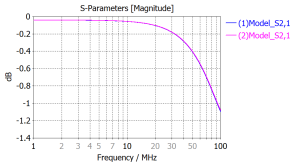
更に、前述③に述べた不要輻射(EMI)関係は伝送路の形態(活線やGNDの各パターン)や寸法、更には信号(ノイズ)の周波数に依存するため、今回のモデルだけから結論を出すことは難しく、場合に合わせて検討すべき、となります。
但し、GND電極パターンを広くしたから不要輻射が低減するというのは、少しステレオタイプ的で、やはり対向する活線側のパターン形状も考慮すべきです。活線側のパターン形状で共振(定在波)が起きている状況では、GND側でも同時に共振(定在波)を起こしていることを意味し、GND電極パターンを広くしたから共振が起きないということにはならないのです。
こう言った信号ライン、電源ラインにおける共振抑制には当社のSD適用、PD適用といった考え方を是非ご検討して頂きたいです。これらはシミュレーションで行いますので、ノイズ抑制効果(ノイズ輻射量の数値化は不可)を数値で検討できますし、素子の調整も可能でEMC設計として回路図設計段階での検討が可能となります。
EMC関連のハウツー本等の中で著者のイメージからGND電極パターンについて解説している記事もあったりしますが、Simをしてみるとその思い込みのイメージとは異なっていることが分かります。当社は“EMC設計 MBDでDX! 技術&学術”の セミナーでGND電極について解説しております。こちらも是非ご検討下さい。
少し話題がズレますが、活線とGNDとはそれぞれ異なる方向に電流が流れるという考え方から、活線とGND間には所謂“フレミング左手の法則の力”による斥力が生じていると考えている方も居られるようですが、前述したように活線とGNDには異なる極性の電荷が移動することからそれらの電荷による“クーロンの法則の力”(引力)が働くので、先ほどの斥力はキャンセルされるとも言えるのです。理屈っぽい話になりましたが、結局のところ、実際の活線とGNDの間には引力も斥力も存在しません。
※関連ページ



